剑指offer016 数值的整数次方

Posted on 2020-01-25 In 剑指offer Valine:

Problem:

给定一个 double 类型的浮点数 base 和 int 类型的整数 exponent，求 base 的 exponent 次方。

Intuition:

这个题目的第一反应是不是一个for循环就搞定了吗？然后写下下面一段代码


public double Power(double base, int exponent){
	double result = 1.0;
	for (int i = 1; i <= exponent; i++) {
		result *= base;
	}
	return result;
}

但是这样是明显会被面试官diss的，指数部分为0或者小于0的时候都没有处理，底数指数均为0的时候也没有抛出异常。

Solution:

// 指数为正数的情况
public double powerWithExponent(double base, int exponent) {
	double result = 1.0;
	for (int i = 1; i <= exponent; i++) {
		result *= base;
	}
	return result;
}
 
// 数值比较的方法
public boolean equal(double num1, double num2) {
	if (Math.abs(num1 - num2) < 0.0000001) {
		return true;
	} else {
		return false;
	}
}
 
// 数值的整数次方
public double power(double base, int exponent) {
	double result = 0.0;
	// 首先比较底数为0,指数为负数的情况，这种情况没有意义
	if (this.equal(base, 0.0) && exponent < 0) {
		try {
			throw new Exception("没有意义");
		} catch (Exception e) {
			e.printStackTrace();
		}
	}
	// exponent的三种情况
	if (exponent == 0) { // exponent为0的情况
		return 1.0;
	} else if (exponent < 0) { // exponent小于0的情况
		result = this.powerWithExponent(1 / base, -exponent);
	} else if (exponent > 0) { // exponent大于0的情况
		result = this.powerWithExponent(base, exponent);
	}
	return result;
}

剑指offer015 二进制中1的个数

Posted on 2020-01-25 In 剑指offer Valine:

Problem:

输入一个整数，输出该数二进制表示中 1 的个数。

Intuition:

这一题考的就是位运算了，这里求解的时候有几个点要注意。首先，千万不要用除法。除法效率比位运算低得多，面试官看到了肯定要扣分。其二，一定要注意负数符号扩展的情况，比如下面这段代码就是错误的

public int numberOf1(int n) {
        int count = 0;
        while (n != 0) {
            if ((n & 1) != 0) {
                ++count;
            }
            n = n >> 1;
        }
        return count;
}

因为如果数字是负数的话，符号位是1.我们对原来的数字不断按位右移得到的是0XFFFFFFFF，不但无法得到正确结果还会进入死循环，正确的做法是移动标志位，代码如下。

Solution:

public int numberOfs1(int n) {
      int count = 0;
      int flag = 1;
      while (flag != 0) {
          if ((n & flag) != 0) {
              ++count;
          }
          flag = flag << 1;
      }
      return count;
  }

剑指offer014 剪绳子

Posted on 2020-01-25 In 剑指offer Valine:

Problem:

把一根绳子剪成多段，并且使得每段的长度乘积最大。

Intuition:

这一题比较容易，算是动态规划的开胃菜。首先我们聊一聊什么样的问题适合用动态规划。动态规划通常适合于要求我们求一个问题的最优解（通常是最大值或者最小值），而且该问题能够分解成若干个字问题，并且子问题之间还有重叠的更小的子问题，就可以考虑用动态规划来解决这个问题。下面的解法我们自己实现的方案既用了贪心算法的思想，也用了动态规划的思想。我们发现仅仅由dp[i-2],dp[i-3]就可以决定dp[i]里面的内容，原因是dp[i-p]（p>3）里面的内容一定是可以由dp[i-2]和dp[i-3]来表示的。举个简单的例子，如果最优解是要用到dp[i-4],那么接下里剩下的4肯定是切成22，那么这种情况就与dp[i-2]2的情况是完全一致的。如果是dp[i-5],那么剩下对于5的切法一定是23,这个和dp[i-2]3或者dp[i-3]*2就是一致的。依次类推，这时属于贪心算法的内容。接下来就用动态规划来存之前计算的结果就可以了。

Solution:

//dynamic programming+greedy algorithm
   public int cutRope(int length){
   	//dp[i]表示的就是长度为i的绳子对应的最大乘积，dp[0]没有意义
       int[] dp=new int[length+1];
       dp[0]=0;
       dp[1]=1;
       dp[2]=2;
       dp[3]=3;
       if (length <= 3) {
           return dp[length];
       }
       for(int i=4;i<=length;i++){
           //这里我们不用再写dp[i-4]*4的原因是dp[i-2]>=dp[i-4]*2,所以dp[i-4]的情况已经被包含在dp[i-2]的情况中了。
           dp[i]=Math.max(dp[i-2]*2,dp[i-3]*3);
       }
       return dp[length];
   }

   public int cutRope_D(int length) {

       if (length < 2) {
           return 0;
       }
       if (length == 2) {
           return 1;
       }
       if (length == 3) {
           return 2;
       }
       // 将最优解存储在数组中
       int[] products = new int[length + 1];
       // 数组中第i个元素表示把长度为i的绳子剪成若干段之后的乘积的最大值
       products[0] = 0;
       products[1] = 1;
       products[2] = 2;
       products[3] = 3;

       int max = 0;

       for (int i = 4; i <= length; i++) {
           max = 0;
           // 求出所有可能的f(j)*f(i-j)并比较出他们的最大值
           for (int j = 1; j <= i / 2; j++) {
               int product = products[j] * products[i - j];
               if (product > max) {
                   max = product;
               }
               products[i] = max;
           }
       }
       max = products[length];

       return max;
   }

剑指offer013机器人的运动范围

Posted on 2020-01-23 In 剑指offer Valine:

Problem:

地上有一个 m 行和 n 列的方格。一个机器人从坐标 (0, 0) 的格子开始移动，每一次只能向左右上下四个方向移动一格，但是不能进入行坐标和列坐标的数位之和大于 k 的格子。

例如，当 k 为 18 时，机器人能够进入方格 (35,37)，因为 3+5+3+7=18。但是，它不能进入方格 (35,38)，因为 3+5+3+8=19。请问该机器人能够达到多少个格子？

Intuition:

使用深度优先搜索（Depth First Search，DFS）方法进行求解。回溯是深度优先搜索的一种特例，它在一次搜索过程中需要设置一些本次搜索过程的局部状态，并在本次搜索结束之后清除状态。这一题和前面一题比较类似，机器人从坐标(0,0)开始移动，当它准备进入坐标为(i,j)的格子时，通过检查坐标的数位和来判断机器人是否能够进入。如果机器人能够进入坐标为（i，j）的格子，再判断它是否能够进入4个相邻的格子（i,j-1）,(i-1,j),(i,j+1),(i+1,j)。设置visited数组的原因是为了避免重复访问导致进入死循环，我们保证如果一个点已经被访问过它就不会再被check了从而保证程序能够在有限时间内退出。

Solution:

public class CodingInterview_013 {
    public int movingCount(int threshold, int rows, int cols) {
        if(threshold <= 0 || rows <= 0 || cols <= 0)
            return 0;

        boolean[] visitFlags = new boolean[rows * cols];    // 元素是否访问过标识

        return movingCountCore(threshold, rows, cols, 0, 0, visitFlags);
    }

    public int movingCountCore(int threshold, int rows, int cols,
                               int row, int col, boolean[] visitFlags) {
        int count = 0;
        // 如果当前元素符合条件，则判断该元素相邻的4个元素
        if(check(threshold, rows, cols, row, col, visitFlags)) {
            int index = row * cols + col;
            visitFlags[index] = true;
            count = 1 + movingCountCore(threshold, rows, cols, row, col + 1, visitFlags) +
                    movingCountCore(threshold, rows, cols, row, col - 1, visitFlags) +
                    movingCountCore(threshold, rows, cols, row + 1, col, visitFlags) +
                    movingCountCore(threshold, rows, cols, row - 1, col, visitFlags);
        }
        return count;
    }

    // 判断row,col的元素是否符合要求
    public boolean check(int threshold, int rows, int cols,
                         int row, int col, boolean[] visitFlags) {
        int index = row * cols + col;
        // 索引值在有效范围内、元素尚未访问、各位数和小于等于阈值
        if(row >= 0 && row < rows && col >= 0 && col < cols &&
                !visitFlags[index] && (getDigitsSum(row) + getDigitsSum(col)) <= threshold ) {
            return true;
        }
        return false;
    }

    // 计算num的各位数和
    public int getDigitsSum(int num) {
        if(num <= 0)
            return 0;
        int sum = 0;
        while(num > 0) {
            sum += num % 10;
            num /= 10;
        }
        return sum;
    }

}

剑指offer012矩阵中的路径

Posted on 2020-01-23 In 剑指offer Valine:

Problem:

判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向上下左右移动一个格子。如果一条路径经过了矩阵中的某一个格子，则该路径不能再进入该格子。

Intuition:

使用回溯法（backtracking）进行求解，它是一种暴力搜索方法，通过搜索所有可能的结果来求解问题。回溯法在一次搜索结束时需要进行回溯（回退），将这一次搜索过程中设置的状态进行清除，从而开始一次新的搜索过程。在这一题中我们要做的是额外用一个数组来记录矩阵中的点是否被访问过的状态。
个人理解回溯法主要适用于程序需要你进行尝试的情况。那么我们在尝试一步后会修改某些状态，那么在尝试不成功的时候要注意对这些状态进行复原。这个过程颇类似于函数调用的时候对程序上下文进行压栈的情况。

Solution:

public class CodingInterview_012 {
    //这一题的重点是要把握好要有一个visited数组来记录哪些地方已经走过。已经走过的点不能被重新访问
    public static boolean hasPath(char[] matrix, int rows, int cols, char[] str) {
        // 参数校验
        if (matrix == null || matrix.length != rows * cols || str == null || str.length < 1) {
            return false;
        }

        // 变量初始化
        boolean[] visited = new boolean[rows * cols];
        for (int i = 0; i < visited.length; i++) {
            visited[i] = false;
        }

        // 记录结果的数组，
        int pathLength = 0;
        // 以每一个点为起始进行搜索
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                if (hasPathCore(matrix, rows, cols, str, visited, i, j, pathLength)) {
                    return true;
                }
            }
        }

        return false;
    }

    /**
     * 回溯搜索算法
     *
     * @param matrix     输入矩阵
     * @param rows       矩阵行数
     * @param cols       矩阵列数
     * @param str        要搜索的字符串
     * @param visited    访问标记数组
     * @param row        当前处理的行号
     * @param col        当前处理的列号
     * @param pathLength 已经处理的str中字符个数
     * @return 是否找到 true是，false否
     */
    private static boolean hasPathCore(char[] matrix, int rows, int cols, char[] str, boolean[] visited,
                                       int row, int col, int pathLength) {

        if (pathLength == str.length) {
            return true;
        }

        boolean hasPath = false;

        // 前面两个条件判断位置是否合法
        //第三个条件判断矩阵位置的当前字符是否与字符串中对应位置的字符一致
        //第四个条件是重点，我们要看这个矩阵位置上的字符是否已经被访问过。
        if (row >= 0 && row < rows
                && col >= 0 && col < cols
                && matrix[row * cols + col] == str[pathLength]
                && !visited[row * cols + col]) {
            //跑到这里说明当前矩阵中的字符与字符串对应位置的字符一致，那么我们就把visit状态置为true,但是此时并不能说明就一定成功，还要看后面的字符能不能满足，
            //一旦不满足还要重新置回false.
            visited[row * cols + col] = true;
            pathLength++;

            // 按左上右下进行回溯
            hasPath = hasPathCore(matrix, rows, cols, str, visited, row, col - 1, pathLength)
                    || hasPathCore(matrix, rows, cols, str, visited, row - 1, col, pathLength)
                    || hasPathCore(matrix, rows, cols, str, visited, row, col + 1, pathLength)
                    || hasPathCore(matrix, rows, cols, str, visited, row + 1, col, pathLength);

            if (!hasPath) {
                //程序执行到了这里就说明当前这个点已经走不通了，需要把它的visit状态重新置回false.
                pathLength--;
                visited[row * cols + col] = false;
            }

        }

        return hasPath;
    }

}

剑指offer011 旋转数组的最小数字

Posted on 2020-01-15 In 剑指offer Valine:

Problem:

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个非递减排序的数组的一个旋转，输出旋转数组的最小元素。

Intuition:

此时问题的关键在于确定对半分得到的两个数组哪一个是旋转数组，哪一个是非递减数组。我们很容易知道非递减数组的第一个元素一定小于等于最后一个元素。那么对于初始情况来说，一个是非递减数组和一个旋转数组。其中最小的数肯定在旋转数组中，那么我们每次二分法都扔掉递增数组，只保留旋转数组。同时保证递增数组中最小的数字（也是第一个元素）被留下来。

通过修改二分查找算法进行求解（l 代表 low，m 代表 mid，h 代表 high）：

当 nums[m] <= nums[h] 时，表示 [m, h] 区间内的数组是非递减数组，[l, m] 区间内的数组是旋转数组，此时令 h = m；
否则 [m + 1, h] 区间内的数组是旋转数组，令 l = m + 1。

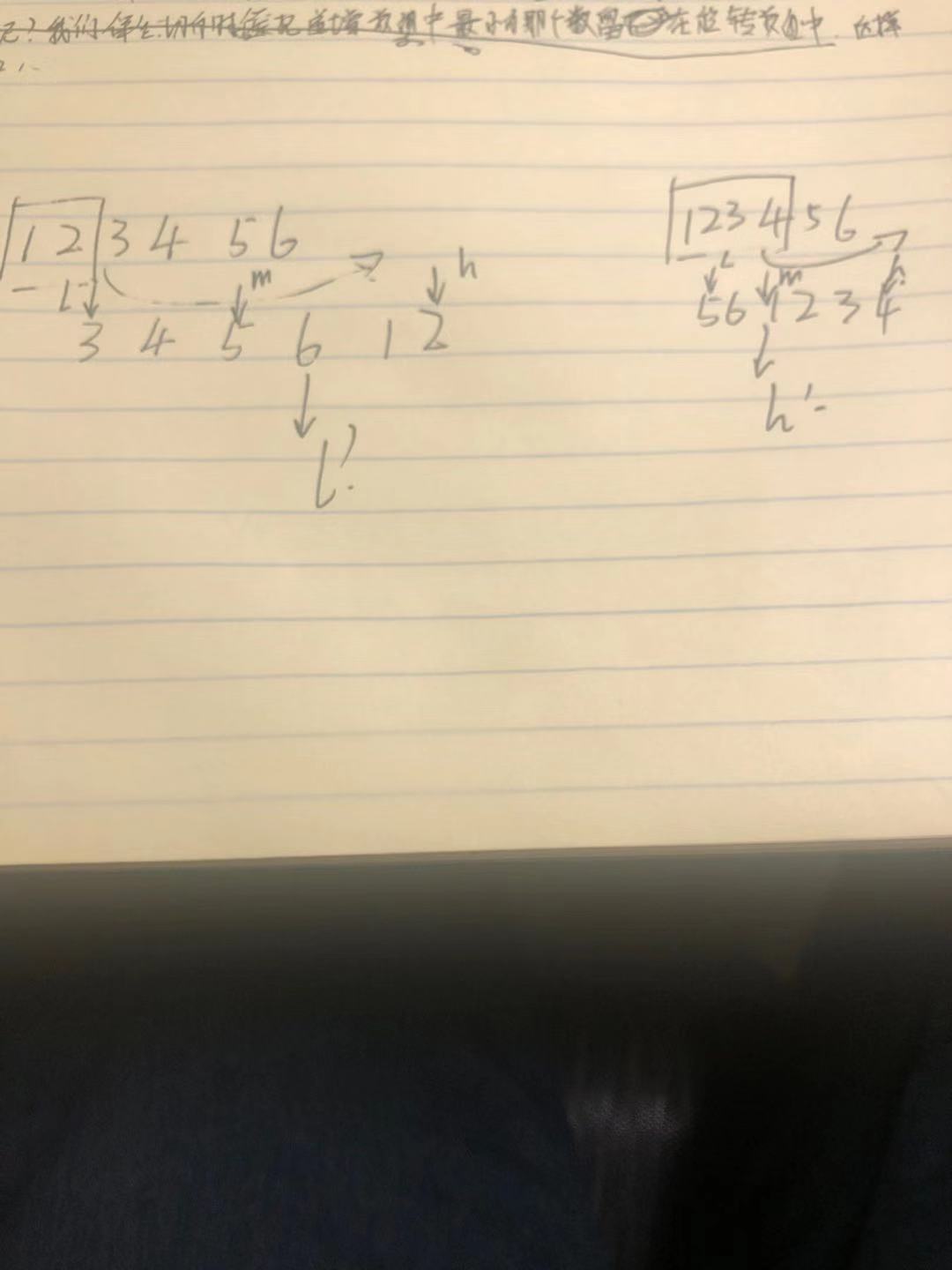
public int minNumberInRotateArray(int[] nums) {
        if (nums.length == 0)
            return 0;
        int l = 0, h = nums.length - 1;
        while(l<h){
            int mid=(l+h)/2;
            //h=mid就是保留下了递增数组中最小的数字
            if(nums[mid]<=nums[h]){
                h=mid;
            }else{
                l=mid+1;
            }
        }
        return nums[l];
    }

做到上面这里核心思路也就完成了，面试官应该也比较满意了，但是解法中还有一点没有考虑到。如果数组元素允许重复，会出现一个特殊的情况：nums[l] == nums[m] == nums[h]，此时无法确定解在哪个区间，需要切换到顺序查找。例如对于数组 {1,1,1,0,1}，l、m 和 h 指向的数都为 1，此时无法知道最小数字 0 在哪个区间。

public int minNumberInRotateArray(int[] nums) {
    if (nums.length == 0)
        return 0;
    int l = 0, h = nums.length - 1;
    while (l < h) {
        int m = l + (h - l) / 2;
        if (nums[l] == nums[m] && nums[m] == nums[h])
            return minNumber(nums, l, h);
        else if (nums[m] <= nums[h])
            h = m;
        else
            l = m + 1;
    }
    return nums[l];
}

private int minNumber(int[] nums, int l, int h) {
    for (int i = l; i < h; i++)
        if (nums[i] > nums[i + 1])
            return nums[i + 1];
    return nums[l];
}

剑指offer10.4 变态跳台阶

Posted on 2020-01-14 In 剑指offer Valine:

Problem:

一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级… 它也可以跳上 n 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

Intuition:

数学推导
跳上 n-1 级台阶，可以从 n-2 级跳 1 级上去，也可以从 n-3 级跳 2 级上去…，那么

f(n-1) = f(n-2) + f(n-3) + … + f(0)
同样，跳上 n 级台阶，可以从 n-1 级跳 1 级上去，也可以从 n-2 级跳 2 级上去… ，那么

f(n) = f(n-1) + f(n-2) + … + f(0)
综上可得

f(n) - f(n-1) = f(n-1)
即

f(n) = 2*f(n-1)
所以 f(n) 是一个等比数列

solution:

1
2
3

public int JumpFloorII(int target) {
    return (int) Math.pow(2, target - 1);
}

剑指offer010_3 跳台阶

Posted on 2020-01-14 In 剑指offer Valine:

Problem:

一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

Intuition:

跳 n 阶台阶，可以先跳 1 阶台阶，再跳 n-1 阶台阶；或者先跳 2 阶台阶，再跳 n-2 阶台阶。而 n-1 和 n-2 阶台阶的跳法可以看成子问题，该问题就又可以转化成斐波那契数列的问题了。

Solution:

public int JumpFloor(int n) {
    if (n <= 2)
        return n;
    int pre2 = 1, pre1 = 2;
    int result = 0;
    for (int i = 2; i < n; i++) {
        result = pre2 + pre1;
        pre2 = pre1;
        pre1 = result;
    }
    return result;
}

剑指offer10.2 矩形覆盖

Posted on 2020-01-14 In 剑指offer Valine:

Problem:

我们可以用 21 的小矩形横着或者竖着去覆盖更大的矩形。请问用 n 个 21 的小矩形无重叠地覆盖一个 2*n 的大矩形，总共有多少种方法？

Intuition:

这个问题就是一个地地道道的斐波那契数列的问题，但是因为隐藏的比较深，看题的时候可能第一时间没办法发现这个事实。不过我们可以做到的是看到这个题第一时间反应过来这是一个递归的问题。我们可以轻易发现n=1时只有一种摆法，n=2时只有两种摆法。如果n>2,那么我们考虑整个图形的左上角。如果左上角的矩形是竖着摆的，那么这种情况就是f(n-1).如果左上角的矩形时横着摆的（21），那么我们可以发现它的下面也必须是一个横着摆的矩形。这样上下两个矩形一起就会拼成一个22的矩形，那么这种情况就是f(n-2)。鉴于左上角的矩形只有两种摆法情况（横着摆或者竖着摆），所以这个问题就被完全转化成了一个斐波那契数列的问题。

Solution:

public int RectCover(int n) {
    if (n <= 2)
        return n;
    int pre2 = 1, pre1 = 2;
    int result = 0;
    for (int i = 3; i <= n; i++) {
        result = pre2 + pre1;
        pre2 = pre1;
        pre1 = result;
    }
    return result;
}

剑指offer010 斐波那契数列

Posted on 2020-01-14 In 剑指offer Valine:

Problem:

求斐波那契数列的第 n 项，n <= 39。

Intuition:

斐波那契数列很适合使用动态规划来求解,它在数学上是使用递归来定义的,公式为F(n) = F(n-1) + F(n-2).
使用动态规划来将重复计算的结果具有”记忆性”,就可以将时间复杂度降低为O(n).

Solution:

public class Solution {

    private int[] fib = new int[40];

    public Solution() {
    	fib[0]=1;
        fib[1] = 1;
        for (int i = 2; i < fib.length; i++)
            fib[i] = fib[i - 1] + fib[i - 2];
    }

    public int Fibonacci(int n) {
        return fib[n];
    }
}