剑指offer002 二维数组查找

Problem:

给定一个二维数组，其每一行从左到右递增排序，从上到下也是递增排序。给定一个数，判断这个数是否在该二维数组中。

Consider the following matrix:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]

Given target = 5, return true.
Given target = 20, return false.
Copy to clipboardErrorCopied
要求时间复杂度 O(M + N)，空间复杂度 O(1)。其中 M 为行数，N 为 列数。

Intuition:

该二维数组中的一个数，小于它的数一定在其左边，大于它的数一定在其下边。因此，从右上角开始查找，就可以根据 target 和当前元素的大小关系来缩小查找区间，当前元素的查找区间为左下角的所有元素。

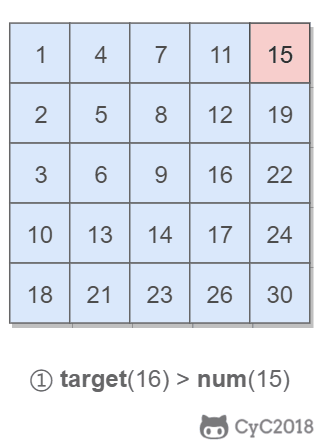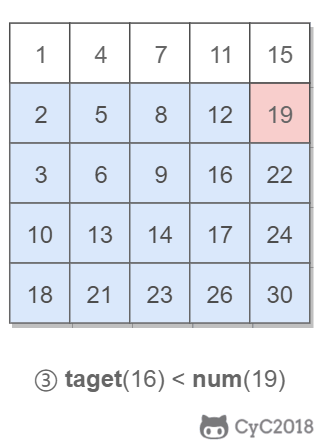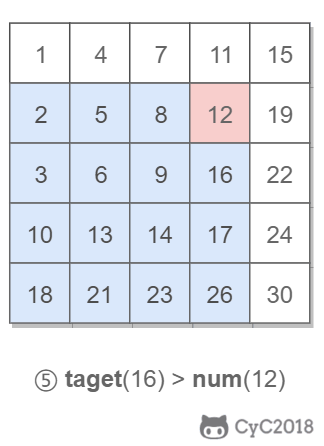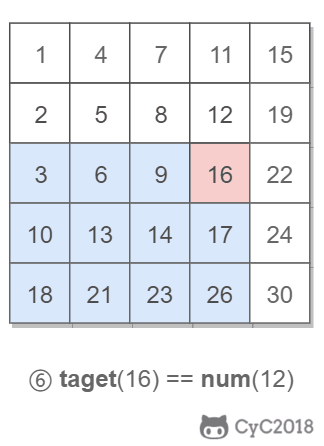
Solution:

 public class CodingInterview_002 {
    public static void main(String[] args) {
        int[][] arr=new int[][]{ {1,   4,  7, 11, 15}, {2,   5,  8, 12, 19}, {3,   6,  9, 16, 22}, {10, 13, 14, 17, 24}, {18, 21, 23, 26, 30}};
        System.out.println(Find(16,arr));
    }
    public static boolean Find(int target, int [][] matrix) {
       if(matrix==null||matrix.length==0||matrix[0].length==0){
           return false;
       }
       //从右上角出发,想到这个是本题的重点。一般习惯性都会考虑从左上角或者右下角出发开始写循环
        // 本题从右上角出发的原因是每一行从左到右递增排序，从上到下也是递增排序。这就意味着只要向左走数字就会减少，向下数字就会变大。
       int row=0;
       int col=matrix[0].length-1;
       while(row<=matrix.length-1&&col>=0){
           if(target==matrix[row][col]){
               return true;
           }else if(target>matrix[row][col]){
               row++;
           }else{
               col--;
           }
       }
       return false;
    }
}